合理的は望ましい??パレート最適とナッシュ均衡3
このように、囚人のジレンマの状況では「お互いが合理的に動いた」結果、「2人にとって悪い結果」になってしまった。
では、2人とも自白しようとしている状態から、2人とも黙秘するという、お互いにとって良い結果があるとわかったのだから、パレート最適である状態であるその状態に移ることはできないのだろうか?そうすれば2人にとって望ましいではないか…
しかしこれはできないのだ。
今はお互い連絡を取ることはできない。とすると、「2人とも自白」から「2人とも黙秘」という結果に移動するには、下の斜めの矢印のような1歩の移動ではなく、2つの矢印が合わさった2歩の移動しかできないのだ。
(上へはルパンが自白から黙秘に行動を変えることで、左へは次元が自白から黙秘に行動を変えることで、それぞれ移動できる。)
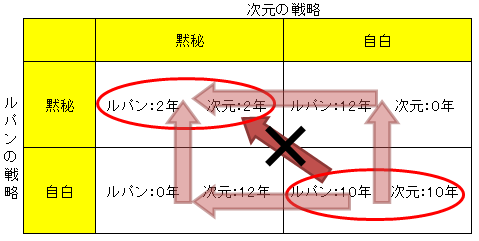
ルパンも次元も「2人とも自白」という状態から「自分だけが行動を変える」と損をしてしまうので、相手の出方がわからない中では、合理的に判断した場合に、自白に変えることはできず、こうして2人とも自白という状態から、このままでは抜け出すことができないのだ。
このような「みんながみんな、自分だけが行動を変えても、得をしない状態」のことをナッシュ均衡という。ナッシュ均衡はゲーム理論で考えたときに起こる結果(ゲームの解)だ。つまりナッシュ均衡がわかれば、そのゲームで起こる結果が予想できる。そして、今回のように、お互いが支配戦略をとった結果は、必ずナッシュ均衡になる。
ここまで見て分かるとおり、2人にとって望ましいとされるパレート最適な状態と、2人が合理的に動いた結果のナッシュ均衡は、一致するとは限らない。そして、一度ナッシュ均衡に陥ってしまうと、均衡という言葉の通り、2人にとってより良い結果がたとえあったとしても、残念ながら、このままでは脱出不可能なのだ。
