タクシー代を割り勘してみよう!
ここでは、今まで見てきた配分や、シャプレー値の求め方、コアの確認の練習をしてみよう。
考え方はわかったし、計算までは必要ないという人は、飛ばしてしまおう。
飲み会の帰り道、不意に大雨が振り出した。そこで、だいたい同じ方向に家があるA、B、Cの3人は、それぞれの家までタクシーを相乗りすることにした。別々にタクシーで帰るより、相乗りした方がお得だからだ。
タクシーの運転手に訪ねたところ、料金は、次の通りのようだ。
「Aだけで自宅まで帰ると1,400円、Bだけだと2,000円、Cだけだと1,600円かかる。AとBが相乗りすると2人で2,500円、BとCが相乗りすると3,000円、CとAが相乗りすると、2,400円。さらに全員で乗っていくと3人で3,800円かかる。」
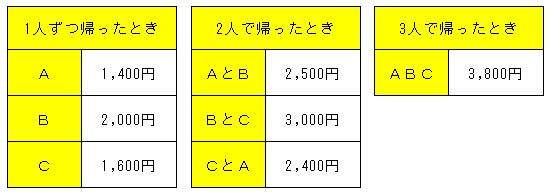
この状態では、1人で別々に帰ると1,400+2,000+1,600=5,000円だが、3人で乗ると3,800円ですむ。1,200円ほど節約が可能なわけだ。2人で乗った場合は、例えばAとBであればひとりずつだと1,400+2,000=3,400円だが、2,500円で済むので900円の節約だ。こう考えると、どうやら、全員で相乗りするのが最も節約額が大きく合理的なようだ。
そこで、A、B、Cは3人で相乗りし、後で割り勘することにした。
では、3,800円をA、B、Cの3人はどのように割り勘すれば良いだろうか?金額が小さいのでけち臭い気もするが、均等配分(平均的正義)、比例配分(配分的正義)、シャプレー値による配分(貢献度で配分)の3つの配分案を計算してみよう。そして、それぞれの配分案がコアになっているのか、確認してみてほしい。
◆均等配分
3人が相乗りすることで5,000-3,800=1,200円ほど節約できた。これを、それぞれに平等に配分する。つまり、ひとりあたり、1,200÷3=400円の節約だ。そのため、次のように求めることができる。
A:1,400-400=1,000円
B:2,000-400=1,600円
C:1,600-400=1,200円
これは、同じ方向の人が3人集まったおかげで安くなったんだから、みんなで同じようにその恩恵にあずかろう、という分け方だ。
◆比例配分
3人の相乗りによって1,200円の出費が減る。これを、それぞれひとりで帰った場合の費用の割合で配分する。1,200円の分け方は、次のように求めることができる。
A:1,200×1,400/(1,400+2,000+1,600)=420円
B:1,200×2,000/(1,400+2,000+1,600)=600円
C:1,200×1,600/(1,400+2,000+1,600)=480円
最終的な出費額は、次のとおりだ。
A:1,400-420=980円
B:2,000-600=1,400円
C:1,600-480=1,120円
これは「長距離の人のほど、節約分は大きいだろう」という考え方だ。それぞれの支払いは、全員同じ割合で30%減っていることがわかるだろう。比例配分は、元々の支払いが大きい人ほど得をする仕組みだ。
◆シャプレー値による配分
まずは、A→B→Cという順番で加わったときを考えてみよう。タクシー代の支払いが自分が加わることでどれだけ変わるのか?という貢献度を見るわけだ。
まず、Aだけなら1,400円なのでAの貢献分は1,400円。
そこにBが加わると、2,500円となる。1,400円から1,100円増えたのでBの貢献分は1,100円。
そこにCが加わると3,800円となる。2,500円から1,300円増加したからCの貢献分は1,300円。
同じように、すべての順番を考えて、次のように平均を求めるシャプレー値が求まる。
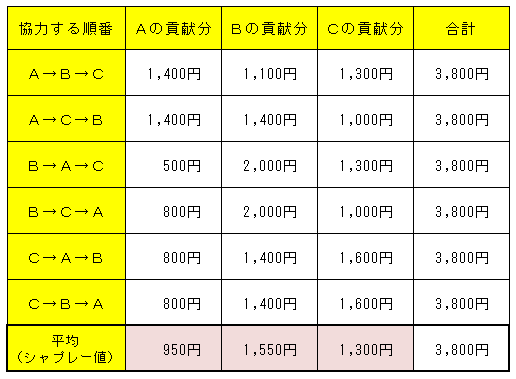
つまり、配分額は次のようになる。
A:950円
B:1550円
C:1300円
これは、単純な平均と違い、「どの程度、帰り道の方向が一緒なのか?」といった貢献度も考慮した配分の方法だ。
次にそれぞれの配分方法がコアかどうかを確認しよう。
コアは「その割り勘の提案なら、2人だけで相乗りする(もしくは1人で帰る)方が得だ」と言われることがない状態であり、つまり、誰もが「抜け駆けしよう」とは思わない提案だ。
コアを求めるときは、条件を数式で求めても良いが、それぞれの提案で、「2人(または1人)で抜け駆けした方が得な人はいないよね?」と確認していっても良い。ここでは後者で考えてみよう。
すると、均等配分の提案では、AとBは合わせて2,600円支払う必要があるが、抜け駆けすれば2,500円で済む。つまり、抜け駆けする方が得な人がいるので、この提案はコアではない。同じようにそれぞれの数字を確認していくと比例配分とシャプレー値による配分は、どちらもコアになっている。
これら3つの配分案は、それぞれ、もっともらしい割り勘だと感じるかもしれない。しかし、コアはでない、つまり誰かが必要以上に損をしている提案の可能性もある。シャプレー値の配分もコアではない可能性は理論上ありえるので、ムダな揉め事を起こさないためにも、コアは必ず確認するようにしよう。
