シャプレー値で知る相手と自分の影響力
それでは、シャプレー値を使って影響力を求めてみよう。
先ほどの選挙の例では、選挙前と選挙後で以下のように議席数が変わったのだった。
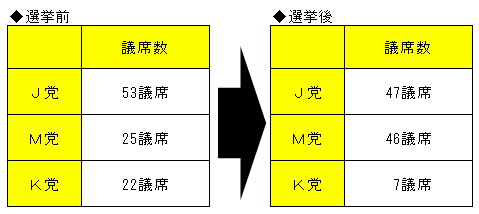
ここでは、引き続き政策は過半数の賛成で決定できるとし、シャプレー値を用いて各党の影響力を計ってみよう。考え方は同じで「自分が加わることでどれだけ結果が良くなるのか」つまり「自分がいなくなるとどれだけ困るのか」を考えていく。
合併と同じように、各党がだんだんと賛成していって過半数を取れたときに決定される。これを100の利得としよう。そして、過半数を取れないなら0の利得として考えてみよう。
まずは選挙前の状態で見てみよう。
基本的な考え方は、企業合併の時と同じだ。まずは、何もない状態からJ→M→Kという順番で賛成に協力していったとしよう。Jが発案して、Mが賛成して、Kが賛成した。という順序だ。
すると、Jが賛成時点で53人ともう過半数の議席を持っているので、Jが賛成した時点で決定される。このときのJの貢献分は100。
そのJにMが賛成に加わって賛成が78人になった。しかし、既に決定しているのでMが加わったところで結果は何も良くなっていない。100→100と変わらないのでMの貢献分は0(100-100)。
さらにKが賛成に加わって全会一致になった。しかし、結局のところ決定しているという結果は変わらないのでKの貢献分もやはり0(100-100)。
これをすべての順番で見て行って平均値を取ればシャプレー値、つまり影響力が次のように求まる。
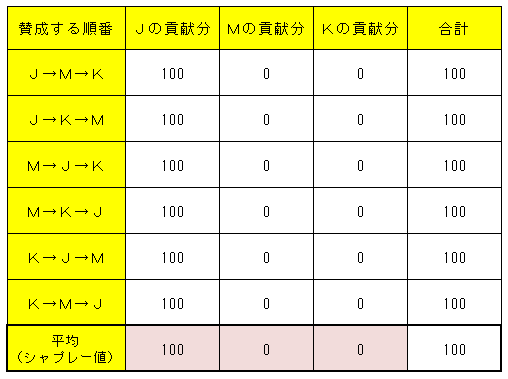
つまり、Jが100%の影響力を持ち、MとKは全く影響力を持っていないという結果になる。J党が過半数の議席を握っており、そして、過半数で決定も拒否もすることができるので当然だ。
では、選挙後はどうなったかを同じように見ていこう。
ここでは、J→K→Mの順に賛成したとしてみてみよう。
Jだけが賛成した時点では、47の賛成では過半数に届かない。つまり、決定はできないので0→0と結果は何も変わっていない。Jの貢献分は0(0-0)。
そこにKが賛成に加わった。すると、今度は54人となり過半数を超えるので決定できる。つまりKが加わることで結果が0→100と良くなったわけだ。Kの貢献分は100(100-0)。
さらにMが賛成に加わって全会一致で賛成になった。しかし、決定しているという結果は何ら変わりない。つまり、Mの貢献分は0(100-100)。
これをすべての順番で行い、平均値を取るとシャプレー値だ。次のように求めることができる。
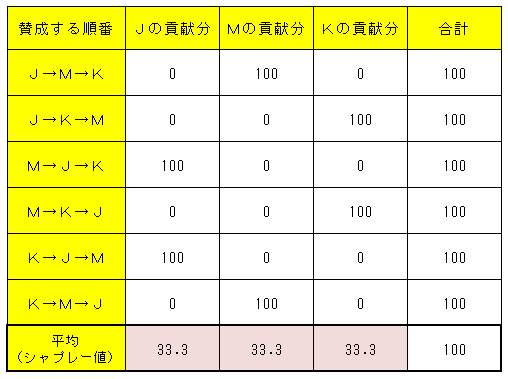
今度はJ、M、Kすべてが33.3%づつ等しく影響力を持っているという結果になっている。つまり、人数はかなり違うのに、実はKは、JやMと同じ影響力を持っているという不思議な結果になるわけだ。
今の状態では、何かを決める際には、2つの党が賛成する必要がある。どの党とどの党でも良く、現在の人数がどうあれ、どの党も他の党の協力がなければ何も決定することはできないという意味で全く同じなのだ。J党の賛成に、K党が加わる際、「47人から54人にちょっと数字が増えただけ」という理解ではなく、「過半数ない状態から過半数ある状態」という劇的な変化を遂げているのだ。
現実は与党が過半数に満たない場合でも、少数政党の数が多かったり、3党以上で連立したりと、少数政党が完全に対等になることは稀である。しかし、うまく立ち回ることで、影響を与えられる状態にすることはできる。
