コラム4 コンビニが密集する謎～ホテリングモデル～2
先ほどの問題では、観光客からすれば②が最もバランス良く見える。
しかし、答えは③で「集客性が多いところにすべて集まって開店する」という結果になる。これは、真ん中より左の客がA、真ん中より右の客がBと、半分ずつ分けるイメージだ。
それでは理由を見てみよう。
スポンサーリンク
商品も価格も同じであれば、アイスクリームが欲しい観光客はより近い方のお店に行くとして、ここで、②の状態を考えてみよう。
海岸の真ん中から右にいる観光客はBの店に、真ん中の線から左にいる観光客はAの店に行き、ちょうど半々だ。
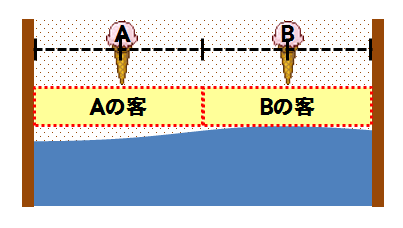
では、このまま落ち着くのか？というと、そうではない。例えばBが左に移動して、下のようになったとしよう。
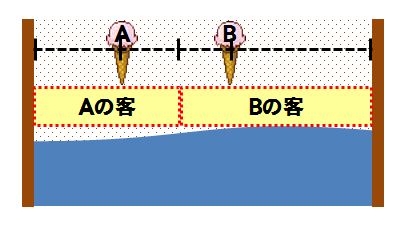
今度はAとB真ん中の線から左がAの客、右がBの客となり、Bは移動することにより客数を増やすことができる。もちろん、Aも黙っていない。Aも移動し…と繰り返していくわけだ。
では、AとB、それぞれがこれ以上移動しても得をしない（つまりナッシュ均衡となっている）位置がどこか？というと、これが③なのだ。③の状態では、AもBも移動すると客が減ってしまう。
例えば、③の状態からBだけ移動したときを考えてみよう。
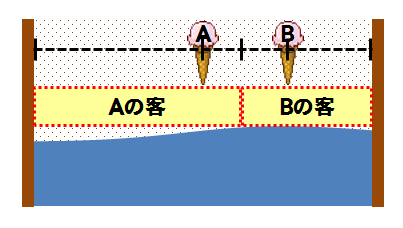
AとBの真ん中の線から左がAの客、右がBの客になってしまう。③の状態では半分半分だったので、これでは損をしてしまう。Aだけが移動したときも同様であり、③の状態では、どちらも移動せずに落ち着くわけだ。
つまり、同じような商品を同じような価格で売る立地競争では、集客性が大きい場所に集まる方が、「競争相手がいない端の方が細々とやるよりも合理的」と言えるのだ。
このように、ホテリングモデルで見ると、コンビニが駅前や大学の前など人が集まるところに複数存在しているのは、ナッシュ均衡の状態であり、合理的に行動した結果だと説明できるわけだ。
スポンサーリンク